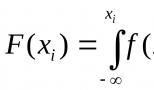Моделирование случайных событий. Разыгрывание непрерывной случайной величины. Метод обратных функций Разыграть пять возможных значений непрерывной случайной величины

Определение 24.1. Случайными числами называют возможные значения r непрерывной случайной величины R , распределенной равномерно в интервале (0; 1).

1. Разыгрывание дискретной случайной величины.

Пусть требуется разыграть дискретную случайную величину Х , то есть получить последовательность ее возможных значений, зная закон распределения Х :

Х х 1 х 2 … х п

р р 1 р 2 … р п .

Рассмотрим равномерно распределенную в (0, 1) случайную величину R и разобьем интервал (0, 1) точками с координатами р 1, р 1 + р 2 , …, р 1 + р 2 +… +р п -1 на п частичных интервалов , длины которых равны вероятностям с теми же индексами.

Теорема 24.1. Если каждому случайному числу , которое попало в интервал , ставить в соответствие возможное значение , то разыгрываемая величина будет иметь заданный закон распределения:

Х х 1 х 2 … х п

р р 1 р 2 … р п .

Доказательство.

Возможные значения полученной случайной величины совпадают с множеством х 1 , х 2 ,… х п , так как число интервалов равно п , а при попадании r j в интервал случайная величина может принимать только одно из значений х 1 , х 2 ,… х п .

Так как R распределена равномерно, то вероятность ее попадания в каждый интервал равна его длине, откуда следует, что каждому значению соответствует вероятность p i . Таким образом, разыгрыываемая случайная величина имеет заданный закон распределения.

Пример. Разыграть 10 значений дискретной случайной величины Х , закон распределения которой имеет вид: Х 2 3 6 8

р 0,1 0,3 0,5 0,1

Решение. Разобьем интервал (0, 1) на частичные интервалы: D 1 - (0; 0,1), D 2 – (0,1; 0,4), D 3 - (0,4; 0,9), D 4 – (0,9; 1). Выпишем из таблицы случайных чисел 10 чисел: 0,09; 0,73; 0,25; 0,33; 0,76; 0,52; 0,01; 0,35; 0,86; 0,34. Первое и седьмое числа лежат на интервале D 1 , следовательно, в этих случаях разыгрываемая случайная величина приняла значение х 1 = 2; третье, четвертое, восьмое и десятое числа попали в интервал D 2 , что соответствует х 2 = 3; второе, пятое, шестое и девятое числа оказались в интервале D 3 – при этом Х = х 3 = 6; на последний интервал не попало ни одного числа. Итак, разыгранные возможные значения Х таковы: 2, 6, 3, 3, 6, 6, 2, 3, 6, 3.

2. Разыгрывание противоположных событий.

Пусть требуется разыграть испытания, в каждом из которых событие А появляется с известной вероятностью р . Рассмотрим дискретную случайную величину Х , принимающую значения 1 (в случае, если событие А произошло) с вероятностью р и 0 (если А не произошло) с вероятностью q = 1 – p . Затем разыграем эту случайную величину так, как было предложено в предыдущем пункте.

Пример. Разыграть 10 испытаний, в каждом из которых событие А появляется с вероятностью 0,3.

Решение. Для случайной величины Х с законом распределения Х 1 0

р 0,3 0,7

получим интервалы D 1 – (0; 0,3) и D 2 – (0,3; 1). Используем ту же выборку случайных чисел, что и в предыдущем примере, для которой в интервал D 1 попадают числа №№1,3 и 7, а остальные – в интервал D 2 . Следовательно, можно считать, что событие А произошло в первом, третьем и седьмом испытаниях, а в остальных – не произошло.

3. Разыгрывание полной группы событий.

Если события А 1 , А 2 , …, А п , вероятности которых равны р 1 , р 2 ,… р п , образуют полную группу, то для из разыгрывания (то есть моделирования последовательности их появлений в серии испытаний) можно разыграть дискретную случайную величину Х с законом распределения Х 1 2 … п, сделав это так же, как в пункте 1. При этом считаем, что

р р 1 р 2 … р п

если Х принимает значение х i = i , то в данном испытании произошло событие А i .

4. Разыгрывание непрерывной случайной величины.

а) Метод обратных функций.

Пусть требуется разыграть непрерывную случайную величину Х , то есть получить последовательность ее возможных значений x i (i = 1, 2, …, n ), зная функцию распределения F (x ).

Теорема 24.2. Если r i – случайное число, то возможное значение x i разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F (x ), соответствующее r i , является корнем уравнения

F (x i ) = r i . (24.1)

Доказательство.

Так как F (x ) монотонно возрастает в интервале от 0 до 1, то найдется (причем единственное) значение аргумента x i , при котором функция распределения примет значение r i . Значит, уравнение (24.1) имеет единственное решение: х i = F -1 (r i ), где F -1 - функция, обратная к F . Докажем, что корень уравнения (24.1) является возможным значением рассматриваемой случайной величины Х. Предположим вначале, что x i – возможное значение некоторой случайной величины x, и докажем, что вероятность попадания x в интервал (с, d ) равна F (d ) – F (c ). Действительно, в силу монотонности F (x ) и того, что F (x i ) = r i . Тогда

Следовательно, Значит, вероятность попадания x в интервал (c, d ) равна приращению функции распределения F (x ) на этом интервале, следовательно, x = Х .

Разыграть 3 возможных значения непрерывной случайной величины Х , распределенной равномерно в интервале (5; 8).

F (x ) = , то есть требуется решить уравнение Выберем 3 случайных числа: 0,23; 0,09 и 0,56 и подставим их в это уравнение. Получим соответствующие возможные значения Х :

б) Метод суперпозиции.

Если функция распределения разыгрываемой случайной величины может быть представлена в виде линейной комбинации двух функций распределения:

то , так как при х ®¥ F (x ) ® 1.

Введем вспомогательную дискретную случайную величину Z с законом распределения

Z 1 2 . Выберем 2 независимых случайных числа r 1 и r 2 и разыграем возможное

p C 1 C 2

значение Z по числу r 1 (см. пункт 1). Если Z = 1, то ищем искомое возможное значение Х из уравнения , а если Z = 2, то решаем уравнение .

Можно доказать, что при этом функция распределения разыгрываемой случайной величины равна заданной функции распределения.

в) Приближенное разыгрывание нормальной случайной величины.

Так как для R , равномерно распределенной в (0, 1), , то для суммы п независимых, равномерно распределенных в интервале (0,1) случайных величин . Тогда в силу центральной предельной теоремы нормированная случайная величина при п ® ¥ будет иметь распределение, близкое к нормальному, с параметрами а = 0 и s =1. В частности, достаточно хорошее приближение получается при п = 12:

Итак, чтобы разыграть возможное значение нормированной нормальной случайной величины х , надо сложить 12 независимых случайных чисел и из суммы вычесть 6.

Метод обратных функций

Пусть требуется разыграть непрерывную случай­ную величину X , т. е. получить последовательность ее возможных значений x i (i = 1,2, ...), зная функцию распределения F (х ).

Теорема. Если r i ,-случайное число, то возможное зна­чение x i разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F (х ), соответствующее r i , является корнем уравнения

F (х i )= r i . (»)

Доказательство. Пусть выбрано случайное число r i (0≤r i <1). Так как в интервале всех возможных зна­чений Х функция распределения F (х ) монотонно возра­стает от 0 до 1, то в этом интервале существует, причем только одно, такое значение аргумента х i , при котором функция распределения примет значение r i . Другими словами, уравнение (*) имеет единственное решение

х i = F - 1 (r i ),

где F - 1 - функция, обратная функции у= F (х ).

Докажем теперь, что корень х i уравнения (*) есть возможное значение такой непрерывной случайной вели­чины (временно обозначим ее через ξ , а потом убедимся, что ξ=Х ). С этой целью докажем, что вероятность попа­дания ξ в интервал, например (с, d ), принадлежащий интервалу всех возможных значений X , равна прираще­нию функции распределения F (х ) на этом интервале:

Р (с< ξ < d )= F (d )- F (с ).

Действительно, так как F (х )- монотонно возрастаю­щая функция в интервале всех возможных значений X, то в этом интервале большим значениям аргумента соот­ветствуют большие значения функции, и обратно. Поэтому, если с <х i < d , то F (c )< r i < F (d ), и обратно [учтено, что в силу (*) F (х i )=r i ].

Из этих неравенств следует, чтоесли случайная величина ξ заключена в интервале

с< ξ < d , ξ (**)

то случайная величина R заключена в интервале

F (с )< R < F (d ), (***)

и обратно. Таким образом, неравенства(**) и (***) рав­носильны, а, значит, и равновероятны:

Р (с < ξ< d )=Р [F (с )< R < F (d )]. (****)

Так как величина R распределена равномерно в ин­тервале (0,1), то вероятность попадания R в некоторый интервал, принадлежащий интервалу (0,1), равна его длине (см. гл. XI, § 6, замечание). В частности,

Р [F (с )< R < F (d ) ] = F (d ) - F (с ).

Следовательно, соотношение (****) можно записать в виде

Р (с < ξ< d )= F (d ) - F (с ).

Итак, вероятность попадания ξ в интервал (с, d ) равна приращению функции распределения F (х ) на этом интер­вале, а это означает, что ξ=Х. Другими словами, числа х i , определяемые формулой (*), есть возможные значения величины Х с заданной функцией распределения F (х ), что и требовалось доказать.

Правило 1. х i , непрерывной случайной величины X, зная ее функцию распределения F (х ), надо выбрать случайное число r i приравнять его функции распределения и решить отно­сительно х i , полученное уравнение

F (х i )= r i .

Замечание 1. Если решить это уравнение в явном видене удается, то прибегают к графическим или численным методам.

Пример I. Разыграть 3 возможных значения непрерывной слу­чайной величины X, распределенной равномерно в интервале (2, 10).

Решение. Напишем функцию распределения величины X, рас­пределенной равномерно в интервале (а, b ) (см. гл. XI, § 3, пример):

F (х )= (х-а )/ (b -а ).

По условию, а = 2, b =10, следовательно,

F (х )= (х- 2)/ 8.

Используя правило настоящего параграфа, напишем уравнение для отыскания возможных значений х i , для чего приравняем функцию распределения случайному числу:

(х i -2 )/8= r i .

Отсюда х i =8 r i + 2.

Выберем 3 случайных числа, например, r i =0,11, r i =0,17, r i =0,66. Подставим эти числа в уравнение, разрешенное относительно х i , в итоге получим соответствующие возможные значенияX : х 1 =8·0,11+2==2,88; х 2 =1.36; х 3 = 7,28.

Пример 2. Непрерывная случайная величина Х распределенапопоказательному закону, заданному функцией распределения (параметр λ > 0 известен)

F (х )= 1 - е - λ х (х>0 ).

Требуется найти явную формулу для разыгрывания возможных зна­чений X.

Решение. Используя правило настоящего параграфа, напишем уравнение

1 - е - λ х i

Решим это уравнение относительно х i :

е - λ х i = 1 - r i , или - λ х i = ln (1 - r i ).

х i =1п (1– r i )/λ.

Случайное число r i заключено в интервале (0,1); следовательно, число 1 - r i , также случайное и принадлежит интервалу (0,1). Дру­гими словами, величины R и 1 - R распределены одинаково. Поэтому для отыскания х i можно воспользоваться более простой формулой:

x i =- ln r i /λ.

Замечание 2. Известно, что (см. гл. XI, §3)

В частности,

Отсюда следует, что если известна плотность вероятности f (x ), то для разыгрывания Х можно вместоуравнений F (x i )=r i решить относительно x i уравнение

Правило 2. Для того чтобы найти возможное значение х i (непрерывной случайной величины X, зная ее плот­ность вероятности f (x ) надо выбрать случайное число r i и решить относительно х i , уравнение

или уравнение

где а- наименьшее конечное возможное значение X.

Пример 3. Задана плотность вероятности непрерывной случайной величины Х f (х )=λ (1-λх /2) в интервале (0; 2/λ); вне этого интер­вала f (х )= 0. Требуется найти явную формулу для разыгрывания возможных значений X.

Решение. Напишем в соответствии с правилом 2 уравнение

Выполнив интегрирование и решив полученное квадратное уравнение относительно х i , окончательно получим

Напомним предварительно, что если случайная величина R распределена равномерно в интервале (0,1), то ее математическое ожидание и дисперсия соответственно равны (см. гл. XII, § 1, замечание 3):

M (R )= 1/2, (*)

D (R )= 1/2. (**)

Составим сумму п независимых, распределенных рав­номерно в интервале (0,1) случайных величин R j (j =1, 2, ...,n):

Для нормирования этой суммы найдем предварительно ее математическое ожидание и дисперсию.

Известно, что математическое ожидание суммы слу­чайных величин равно сумме математических ожиданий слагаемых. Сумма (***) содержит п слагаемых, матема­тическое ожидание каждого из которых в силу (*) равно 1/2; следовательно, математическое ожидание суммы (*** )

Известно, что дисперсия суммы независимых случай­ных величин равна сумме дисперсий слагаемых. Сумма (***) содержит n независимых слагаемых, дисперсия каж­дого из которых в силу (**) равна 1/12; следовательно, дисперсия суммы (***)

Отсюда среднее квадратическое отклонение суммы (***)

Пронормируем рассматриваемую сумму, для чего выч­тем математическое ожидание и разделим результат на среднее квадратическое отклонение:

В силу центральной предельной теоремы при п→∞ распределение этой нормированной случайной величины стремится к нормальному с параметрами а= 0 и σ=1. При конечном п распределение прибли­женно нормальное. В частности, при п = 12 получим достаточно хорошее и удобное для расчета приближение

Правило. Для того чтобы разыграть возможное зна­чение x i нормальной случайной величины Х с парамет­рами а=0 и σ=1, надо сложить 12 независимых слу­чайных чисел и из полученной суммы вычесть 6:

Пример, а) Разыграть 100 возможных значений нормальной вели­чины Х с параметрами а=0 и σ=1; б) оценить параметры разыг­ранной величины.

Решение. а) Выберем 12 случайных чисел из первой строки таблицы *) , сложимих и из полученной суммы вычтем 6; в итоге имеем

x i =(0,10+0,09+...+0,67) - 6= - 0,99.

Аналогично, выбирая из каждой следующей строки таблицы пер­вые 12 чисел, найдем остальные возможные значения X.

б) Выполнив расчеты, получим искомые оценки:

Оценки удовлетворительные: а* близко к нулю, σ* мало отличается от единицы.

Замечание. Если требуется разыграть возможное значение z i , нормальной случайной величины Z с математическим ожиданием а и средним квадратическим отклонением σ , то, разыграв по пра­вилу настоящего параграфа возможное значение x i , находят искомое возможное значение по формуле

z i =σx i +a.

Эта формула получена из соотношения (z i -a )/σ=x i .

Задачи

1. Разыграть 6 значений дискретной случайной величины X, закон распределения которой задан в виде таблицы

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,73; 0,75; 0,54; 0,08; 0,28; 0,53. Отв. 10; 10; 10; 2; 3; 22; 10.

2. Разыграть 4 испытания, в каждом из которых вероятность появления события А равна 0,52.

Указание. Для определенности принять, что выбраны слу­чайные числа: 0;28; 0,53; 0,91; 0,89.

Отв. А, , .

3. Заданы вероятности трех событий, образующих полную группу: Р (А 1)=0,20, Р (А 2)=0,32, Р (А 3 )= 0,48. Разыграть 6 испытаний, в каждом из которых появляется одно из заданных событий.

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,77; 0,19; 0,21; 0,51; 0,99; 0,33.

Отв. А 3 , А 1 , А 2 , А 2 , А 3 , А 2 .

4. События А и В независимы и совместны. Разыграть 5 испы­таний, в каждом из которых вероятность появления события А равна 0,5, а события В- 0,8.

А 1 =АВ , для определенности принять случайные числа: 0,34; 0,41; 0,48; 0,21; 0,57.

Отв. А 1 , А 2 , А 2 , А 1 , А 3 .

5. События А, В, С независимы и совместны. Разыграть 4 испы­тания в каждом из которых вероятности появления событий заданы: Р (А )= 0,4, Р (В )= 0,6, Р (С )= 0,5.

Указание. Составить полную группу событий: для определенности принять, что выбраны случайные числа: 0,075; 0,907; 0,401; 0,344.

Отв.А 1 , А 8 , А 4 , А 4 .

6. События А и В зависимы и совместны. Разыграть 4 испытания, в каждом из которых заданы вероятности: Р (А )=0,7, Р (В )=0,6, Р (АВ )=0,4.

Указание. Составить полную группу событий: А 1 =АВ , для определенности принять случайные числа: 0,28; 0,53; 0,91; 0,89.

Отв. А 1 , А 2 , А 4 , А 3 .

7. Разыграть 3 возможных значения непрерывной случайной величины X, которая распределена по показательному закону и задана функцией распределения F (х )= 1 - е -10 x .

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,67; 0,79; 0,91.

Отв. 0,04; 0,02; 0,009.

8. Разыграть 4 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (6,14).

Указание. Для определенности принять, что выбраны слу­чайные числа: 0,11: 0,04; 0,61; 0,93.

Отв. 6,88; 6,32; 10,88; 13,44.

9. Найти методом суперпозиции явные формулы для разыгрывания непрерывной случайной величины X, заданной функцией рас­пределения

F (x )=1- (1/3)(2е- 2 x +е -3 x:), 0<х <∞.

Отв. х= - (1/2)1п r 2 , если r 1 < 2/3; х = - (1/3)1п r 2 , если r 1 ≥2/3.

10. Найти явную формулу для разыгрывания непрерывной слу­чайной величины X, заданной плотностью вероятности f (х )=b /(1 +ax ) 2 в интервале 0≤x ≤1/(b-a ); вне этого интервала f(x)=0.

Отв. х i = - r i /(b - ar i ).

11. Разыграть 2 возможных значения нормальной случайной величины с параметрами: а) а =0, σ =1; б) а =2, σ =3.

Указание. Для определенности принять случайные числа (далее указано число сотых долей; например, числу 74 соответствует слу­чайное число r 1 =0,74): 74. 10, 88, 82. 22, 88, 57, 07, 40, 15, 25, 70; 62, 88, 08, 78, 73, 95, 16, 05, 92, 21, 22, 30.

Отв. а) x 1 = - 0,22, x 2 = - 0.10; 6) z 1 =1,34, z 2 =2,70.

Глава двадцать вторая

Пусть требуется разыграть непрерывную случайную величину X, т.е. получить последовательность ее возможных значений (i=1, 2, ..., n), зная функцию распределения F(x).

Теорема. Если - случайное число, то возможное значение разыгрываемой непрерывной случайной величины X с заданной функцией распределения F (х), соответствующее , является корнем уравнения .

Правило 1. Для того чтобы найти возможное значение , непрерывной случайной величины X, зная ее функцию распределения F (х), надо выбрать случайное число , приравнять его функции распределения и решить относительно полученное уравнение .

Замечание 1. Если решить это уравнение в явном виде не удается, то прибегают к графическим или численным методам.

Пример 1. Разыграть 3 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (2, 10).

Решение: Напишем функцию распределения величины X, распределенной равномерно в интервале (а, b): .

По условию, а=2, b=10, следовательно, .

Используя правило 1, напишем уравнение для отыскания возможных значений , для чего приравняем функцию распределения случайному числу:

Отсюда .

Выберем 3 случайных числа, например, , , . Подставим эти числа в уравнение, разрешенное относительно ; в итоге получим соответствующие возможные значения X: ; ; .

Пример 2. Непрерывная случайная величина X распределена по показательному закону, заданному функцией распределения (параметр известен) (х >0). Требуется найти явную формулу для разыгрывания возможных значений X.

Решение: Используя правило, напишем уравнение .

Решим это уравнение относительно : , или .

Случайное число заключено в интервале (0, 1); следовательно, число - также случайное и принадлежит интервалу (0,1). Другими словами, величины R и 1-R распределены одинаково. Поэтому для отыскания можно воспользоваться более простой формулой .

Замечание 2. Известно, что .

В частности, .

Отсюда следует, что если известна плотность вероятности , то для разыгрывания X можно вместо уравнений решить относительно уравнение .

Правило 2. Для того чтобы найти возможное значение непрерывной случайной величины X, зная ее плотность вероятности , надо выбрать случайное число и решить относительно уравнение или уравнение , где а - наименьшее конечное возможное значение X.

Пример 3. Задана плотность вероятности непрерывной случайной величины X в интервале ; вне этого интервала . Требуется найти явную формулу для разыгрывания возможных значений X.

Решение: Напишем в соответствии с правилом 2 уравнение .

Выполнив интегрирование и решив полученное квадратное уравнение относительно , окончательно получим .

18.7 Приближённое разыгрывание нормальной случайной величины

Напомним предварительно, что если случайная величина R распределена равномерно в интервале (0, 1), то ее математическое ожидание и дисперсия соответственно равны: М(R)=1/2, D(R)=1/12.

Составим сумму n независимых, распределенных равномерно в интервале (0, 1) случайных величин : .

Для нормирования этой суммы найдем предварительно ее математическое ожидание и дисперсию.

Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Сумма содержит n слагаемых, математическое ожидание каждого из которых в силу М(R)=1/2 равно 1/2; следовательно, математическое ожидание суммы

Известно, что дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых. Сумма содержит n независимых слагаемых, дисперсия каждого из которых в силу D(R)=1/12 равна 1/12; следовательно, дисперсия суммы

Отсюда среднее квадратическое отклонение суммы

Пронормируем рассматриваемую сумму, для чего вычтем математическое ожидание и разделим результат на среднее квадратическое отклонение: .

В силу центральной предельной теоремы при распределение этой нормированной случайной величины стремится к нормальному с параметрами а=0 и . При конечном n распределение приближенно нормальное. В частности, при n=12 получим достаточно хорошее и удобное для расчета приближение .

Оценки удовлетворительные: близко к нулю, мало отличается от единицы.

Список использованных источников

1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.:Высшая школа, 2001.

2. Калинина В.Н., Панкин В.Ф. Математическая статистика. – М.: Высшая школа, 2001.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2001.

4. Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика. – М.:ФОРУМ:ИНФРА-М, 2003.

5. Агапов Г.И. Задачник по теории вероятностей. – М.: Высшая школа, 1994.

6. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. – М.: ИНФРА-М, 2001.

7. Вентцель Е.С. Теория вероятностей. – М.: Высшая школа, 2001.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

ЗАНЯТИЕ 1

Моделирование случайных событий с заданным законом распределения

Разыгрывание дискретной случайной величины

Пусть требуется разыграть дискретную случайную величину, т.е. получить последовательность ее возможных значений x i (i = 1,2,3,...n), зная закон распределения X:

Обозначим через R непрерывную случайную величину. Величина R распределена равномерно в интервале (0,1). Через r j (j = 1,2,...) обозначим возможные значения случайной величины R. Разобьем интервал 0 < R < 1 на оси 0r точками с координатами на n частичных интервалов.

Тогда получим:

Видно, что длина частичного интервала с индексом i равна вероятности Р с тем же индексом. Длина

Таким образом, при попадании случайного числа r i в интервал случайная величина Х принимает значение x i с вероятностью P i .

Существует следующая теорема:

Если каждому случайному числу, которое попало в интервал, поставить в соответствие возможное значение x i , то разыгрываемая величина будет иметь заданный закон распределения

Алгоритм разыгрывания дискретной случайной величины заданной законом распределения

1. Нужно разбить интервал (0,1) оси 0r на n частичных интервалов:

2. Выбрать (например, из таблицы случайных чисел, или в компьютере) случайное число r j .

Если r j попало в интервал, то разыгрываемая дискретная случайная величина приняла возможное значение x i .

Разыгрывание непрерывной случайной величины

Пусть требуется разыграть непрерывную случайную величину Х, т.е. получить последовательность ее возможных значений x i (i = 1,2,...). При этом функция распределения F(X) известна.

Существует следующая теорема .

Если r i - случайное число, то возможное значение x i разыгрываемой непрерывной случайной величины Х с известной функцией распределения F(X) соответствующее r i , является корнем уравнения

Алгоритм разыгрывания непрерывной случайной величины:

1. Необходимо выбрать случайное число r i .

2. Приравнять выбранное случайное число известной функции распределения F(X) и получить уравнение.

3. Решить данное уравнение относительно x i . Полученное значение x i будет соответствовать одновременно и случайному числу r i . и заданному закону распределения F(X).

Пример. Разыграть 3 возможных значения непрерывной случайной величины Х, распределенной равномерно в интервале (2; 10).

Функция распределения величины Х имеет следующий вид:

По условию, a = 2, b = 10, следовательно,

В соответствии с алгоритмом разыгрывания непрерывной случайной величины приравняем F(X) выбранному случайному числу r i .. Получим отсюда:

Подставим эти числа в уравнение (5.3).Получим соответствующие возможные значения х:

Задачи на моделирование случайных событий с заданным законом распределения

1. Требуется разыграть 10 значений дискретной случайной величины, т.е. получить последовательность ее возможных значений x i (i=1,2,3,…n), зная закон распределения Х

Выберем из таблицы случайных чисел случайное число r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,66; 0,99; 0,19; 0,88; 0,59; 0,78

2. Периодичность поступления заявок на обслуживание подчинена показательному закону распределения () , x, параметр л известен (в дальнейшем л =1/t - интенсивность поступления заявок)

л=0,5 заявок/час. Определить последовательность значений продолжительности интервалов между поступлениями заявок. Число реализаций равно 5. Число r j: 0,10; 0,12; 0,37; 0,09; 0,65; 0,99;

ЗАНЯТИЕ 2

Система массового обслуживания

Системы, в которых, с одной стороны, возникают массовые запросы на выполнение каких либо видов услуг, а с другой стороны, происходит удовлетворение этих запросов, называются системами массового обслуживания. Любая СМО служит для выполнения потока заявок.

СМО включают в себя: источник требований, входящий поток, очередь, обслуживающее устройство, выходящий поток заявок.

СМО подразделяются:

СМО с потерями (отказами)

СМО с ожиданием (неограниченная длина очереди)

СМО с ограниченной длиной очереди

СМО с ограниченным временем ожидания.

По числу каналов или приборов обслуживания СМО бывают одноканальными и многоканальными.

По месту нахождения источника требований: разомкнутые и замкнутые.

По количеству обслуживающих элементов на одно требование: однофазные и многофазные.

Одной из форм классификации - классификация Д. Кендалла- А/В/X/Y/Z

А - определяет распределение времени между прибытиями;

B - определяет распределение времени обслуживания;

X - определяет количество служебных каналов;

Y - определяет пропускную способность системы (длину очереди);

Z - определяет очередность обслуживания.

Когда пропускная способность системы бесконечна и очередность обслуживания подчиняется принципу «первый пришел -первый обслужился», части Y/Z опускают. В первом разряде (А) используются следующие символы:

М-распределение имеет показательный закон,

G-отсутствие каких-либо предположений о процессе обслуживания, либо он отождествляется с символом GI, означающий рекуррентный процесс обслуживания,

D- детерминированный (время обслуживания фиксированное),

Е n - эрланговское n-ого порядка,

НМ n - гиперэрланговское n-ого порядка.

Во втором разряде (В) используются те же символы.

В четвертом разряде (Y) показывается емкость буфера, т.е. максимальное количество мест в очереди.

В пятом разряде (Z) указывается способ выбора из очереди в системе с ожиданием: SP-равновероятный, FF- первый пришел-первый ушел, LF- последний пришел -первый ушел, PR- приоритетный.

Для задач:

л- среднее количество заявок, поступающих в единицу времени

µ- среднее количество заявок, обслуженных в единицу времени

Коэффициент загрузки 1 канала, или доля времени, когда канал занят.

Основные характеристики:

1) Р отк - вероятность отказа - вероятность того, что система откажет в обслуживании и требование теряется. Это бывает, когда канал или все каналы заняты (ТФоП).

Для многоканальной СМО Р отк =Р n , где n- число каналов обслуживания.

Для СМО с ограниченной длиной очереди Р отк =Р n + l , где l- допустимая длина очереди.

2) Относительная q и абсолютная А пропускная способность системы

q= 1-Р отк А=qл

3) Общее количество требований, находящихся в системе

L сис = n - для СМО с отказами , n- число каналов, занятых обслуживанием.

Для СМО с ожиданием и ограниченной длиной очереди

L сис = n+L ож

где L ож - среднее количество требований, ожидающих начало обслуживания и т.д.

Остальные характеристики рассмотрим по ходу решения задач.

Одноканальная и многоканальная системы массового обслуживания. Системы с отказами.

Простейшей одноканальной моделью с вероятностным входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид

Плотность распределения длительностей обслуживания:

Потоки заявок и обслуживаний простейшие. Пусть система работает с отказами. Этот тип СМО может быть использован при моделировании каналов передачи в локальных сетях. Необходимо определить абсолютную и относительную пропускную способность системы. Представим данную систему массового обслуживания в виде графа (рисунок 2), у которого имеются два состояния:

S 0 - канал свободен (ожидание);

S 1 - канал занят (идет обслуживание заявки).

Рисунок 2. Граф состояний одноканальной СМО с отказами

Обозначим вероятности состояний: P 0 (t) - вероятность состояния «канал свободен»; P 1 (t) - вероятность состояния «канал занят». По размеченному графу состояний составим систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Система линейных дифференциальных уравнений имеет решение с учетом нормировочного условия P 0 (t) + P 1 (t) = 1 . Решение данной системы называется неустановившимся, поскольку оно непосредственно зависит от t и выглядит следующим образом:

P 1 (t) = 1 - P 0 (t) (3.4.3)

Нетрудно убедиться, что для одноканальной СМО с отказами вероятность P 0 (t) есть не что иное, как относительная пропускная способность системы q. Действительно, P 0 - вероятность того, что в момент t канал свободен и заявка, пришедшая к моменту t, будет обслужена, а, следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно P 0 (t), т. е. q = P 0 (t).

По истечении большого интервала времени (при) достигается стационарный (установившийся) режим:

Зная относительную пропускную способность, легко найти абсолютную. Абсолютная пропускная способность (А) - среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:

Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал занят»:

Данная величина P отк может быть интерпретирована как средняя доля не обслуженных заявок среди поданных.

В подавляющем большинстве случаев на практике системы массового обслуживания являются многоканальными, и, следовательно, модели с n обслуживающими каналами (где n>1) представляют несомненный интерес. Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока л, при этом параллельно может обслуживаться не более n клиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется 1/м. Входной и выходной потоки являются пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения. Конечная цель использования n параллельно включенных обслуживающих каналов заключается в повышении (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно n клиентов. Граф состояний многоканальной системы массового обслуживания с отказами имеет вид, показанный на рисунке 4.

Рисунок 4. Граф состояний многоканальной СМО с отказами

S 0 - все каналы свободны;

S 1 - занят один канал, остальные свободны;

S k - заняты ровно k каналов, остальные свободны;

S n - заняты все n каналов, остальные свободны.

Уравнения Колмогорова для вероятностей состояний системы P 0 , ... ,P k , ... P n будут иметь следующий вид:

Начальные условия решения системы таковы:

P 0 (0) = 1, P 1 (0) = P 2 (0) = ... = P k (0) = ... = P 1 (0) = 0 .

Стационарное решение системы имеет вид:

Формулы для вычисления вероятностей P k (3.5.1) называются формулами Эрланга.

Определим вероятностные характеристики функционирования многоканальной СМО с отказами в стационарном режиме:

1) вероятность отказа:

так как заявка получает отказ, если приходит в момент, когда все n каналов заняты. Величина P отк характеризует полноту обслуживания входящего потока;

2) вероятность того, что заявка будет принята к обслуживанию (она же - относительная пропускная способность системы q) дополняет P отк до единицы:

3) абсолютная пропускная способность

4) среднее число каналов, занятых обслуживанием () следующее:

Величина характеризует степень загрузки СМО.

Задачи к занятию 2

1.Ветвь связи, имеющая один канал, принимает простейший поток сообщений с интенсивностью л=0,08 сообщений в секунду. Время передачи распределено по exp закону. Обслуживание одного сообщения происходит с интенсивностью µ=0,1. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения, получают отказ передачи.

Коэфф. Относительной загрузки канала (вероятность занятости канала)

Р отк вероятность отказа приема сообщения

Q относительная пропускная способность межузловой ветви

А абсолютная пропускная способность ветви связи.

2. Ветвь связи имеет один канал и принимает сообщения через каждые 10 секунд. Время обслуживания одного сообщения 5 секунд. Время передачи сообщения распределено по экспоненциальному закону. Сообщения, поступающие в моменты времени, когда канал занят, получают отказ в обслуживании.

Определить

Р зан - вероятность занятости канала связи (коэфф. относительной загрузки)

Q- относительная пропускная способность

А- абсолютная пропускная способность ветви связи

4. Межузловая ветвь вторичной сети связи имеет n = 4 канала. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность = 8 сообщений в секунду. Среднее время передачи одного сообщения равно t = 0,1 cекунд Сообщение прибывшее в момент, когда все n каналов заняты, получает отказ передачи по ветви связи. Найти характеристики СМО:

ЗАНЯТИЕ 3

Одноканальная система с ожиданием

Рассмотрим теперь одноканальную СМО с ожиданием. Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью. Интенсивность потока обслуживания равна (т. е. в среднем непрерывно занятый канал будет выдавать обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания. Данная СМО является наиболее распространенной при моделировании. С той или иной долей приближения с ее помощью можно моделировать практически любой узел локальной вычислительной сети (ЛВС).

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Система М/М/1/N. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость. Граф состояний СМО в этом случае имеет вид, показанный на рисунке 3

Рисунок 3. Граф состояний одноканальной СМО с ожиданием (схема гибели и размножения)

Состояния СМО имеют следующую интерпретацию:

S 0 - «канал свободен»;

S 1 - «канал занят» (очереди нет);

S 2 - «канал занят» (одна заявка стоит в очереди);

S n - «канал занят» (n -1 заявок стоит в очереди);

S N - «канал занят» (N - 1 заявок стоит в очереди).

Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:

где p=коэффициент загрузки

n - номер состояния.

Решение приведенной выше системы уравнений для нашей модели СМО имеет вид:

Начальное значение вероятности для СМО с ограниченной длиной очереди

Для СМО с бесконечной очередью Н =? :

Р 0 =1- с (3.4.7)

Следует отметить, что выполнение условия стационарности для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди, которая не может превышать (N - 1), а не соотношением между интенсивностями входного потока, т. е. не отношением с= л/м.

В отличие от одноканальной системы, которую рассматривали выше и при неограниченной очереди, в этом случае стационарное распределение числа запросов существует при любых конечных значениях коэффициента загрузки с.

Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной (N - 1) (М/М/1/N), а также для одноканальной СМО с буфером неограниченной емкости (М/М/1/?). Для СМО с бесконечной очередью должно выполняться условие с<1, т.е., для того, чтобы в системе не накапливалась бесконечная очередь необходимо, чтобы в среднем запросы в системе обслуживались быстрее, чем они туда поступают.

1) вероятность отказа в обслуживании заявки:

Одной из важнейших характеристик систем, в которых возможна потеря запросов, является вероятность Р loss того, что произвольный запрос будет потерян. При этом вероятность потери произвольного запроса совпадает с вероятностью того, что в произвольный момент времени все места для ожидания заняты, т.е. справедлива формула Р от к = Р Н

2) относительная пропускная способность системы:

Для СМО с неограниченно й очередью q =1, т.к. все заявки будут обслужены

3) абсолютная пропускная способность:

4) среднее число находящихся в системе заявок:

L S с неограниченной очередью

5) среднее время пребывания заявки в системе:

Для неограниченной очереди

6) средняя продолжительность пребывания клиента (заявки) в очереди:

При неограниченной очереди

7) среднее число заявок (клиентов) в очереди (длина очереди):

при неограниченной очереди

Сравнивая выражения для среднего времени ожидания в очереди Т оч и формулу для средней длины очереди L оч, а также среднего времени пребывания запросов в системе Т S и среднего числа запросов в системе L S , видим, что

L оч =л*Т оч L s =л* Т s

Отметим, что эти формулы справедливы и для многих более общих, чем рассматриваемая система М/М/1, систем массового обслуживания и называются формулами Литтла. Практическая значимость этих формул состоит в том, что они избавляют от необходимости непосредственного вычисления величин Т оч и Т s при известном значении величин L оч и L s и наоборот.

Задачи по одноканальной СМО с ожиданием , с ожиданием и ограниченной длиной очереди

1. Дана однолинейная СМО с неограниченным накопителем очереди. Заявки поступают через каждые t =14 секунд. Среднее время передачи одного сообщения t=10 секунд. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят, принимаются в очередь, не покидая ее до начала обслуживания.

Определить следующие показатели эффективности:

2. Межузловая ветвь связи, имеющая один канал и накопитель очереди для m=3 ожидающих сообщений (N-1=m), принимает простейший поток сообщений с интенсивностью л=5 сооб. в сек.. Время передачи сообщений распределено по экспоненциальному закону. Среднее время передачи одного сообщения равно 0,1 секунды. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения и в накопителе отсутствует свободное место, получают отказ.

Р отк - вероятность отказа приема сообщения

L сист - среднее суммарное число сообщений в очереди и передающихся по ветви связи

Т оч - среднее время пребывания сообщения в очереди до начала передачи

Т сист - среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи

Q- относительную пропускную способность

А- абсолютную пропускную способность

3. Межузловая ветвь вторичной сети связи, имеющая один канал и накопитель очереди для m = 4 (N-1=4) ожидающих сообщений, принимает простейший поток сообщений с интенсивностью = 8 сообщений в секунду. Время передачи сообщений распределено по экспоненциальному закону. Среднее время передачи одного сообщения составляет t = 0,1 секунду. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения и в накопителе отсутствует свободное место, получают очереди отказ.

Р отк - вероятность отказа приёма сообщения для передачи по каналу связи межузловой ветви;

L оч - среднее число сообщений в очереди к ветви связи вторичной сети очереди;

L сист - среднее суммарное число сообщений в очереди и передающихся по ветви связи вторичной сети;

Т оч - среднее время пребывания сообщения в очереди до начала передачи;

Р зан - вероятность занятости канала связи (коэфф. относительной загрузки канала);

Q - относительную пропускную способность межузловой ветви;

А - абсолютную пропускную способность межузловой ветви;

4. Межузловая ветвь связи, имеющая один канал и накопитель очереди для m=2 ожидающих сообщений, принимает простейший поток сообщений с интенсивностью л=4 сооб. в сек.. Время передачи сообщений распределено по экспоненциальному закону. Среднее время передачи одного сообщения равно 0,1 секунды. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения и в накопителе отсутствует свободное место, получают отказ.

Определить следующие показатели эффективности ветви связи:

Р отк - вероятность отказа приема сообщения

L оч - среднее число сообщений в очереди к ветви связи

L сист - среднее суммарное число сообщений в очереди и передающихся по ветви связи

Т оч - среднее время пребывания сообщения в очереди до начала передачи

Т сист - среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи

Р зан - вероятность занятости канала связи (коэфф. относительной загрузки канала с)

Q- относительную пропускную способность

А- абсолютную пропускную способность

5. Межузловая ветвь вторичной сети связи, имеющая один канал и неограниченный по объему накопитель очереди ожидающих сообщений, принимает простейший поток сообщений с интенсивностью л= 0,06 сообщений в секунду. Среднее время передачи одного сообщения t =10 секунд. Сообщения, поступающие в моменты времени, когда канал связи занят, принимаются в очередь и не покидают ее до момента начала обслуживания.

Определить следующие показатели эффективности ветви связи вторичной сети:

L оч - среднее число сообщений в очереди к ветви связи;

L сист - среднее суммарное число сообщений в очереди и передающихся по ветви связи;

Т оч - среднее время пребывания сообщения в очереди;

Т сист - среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи;

Р зан - вероятность занятости канала связи (коэффициент относительной загрузки канала);

Q- относительную пропускную способность межузловой ветви;

А- абсолютную пропускную способность межузловой ветви

6. Дана однолинейная СМО с неограниченным накопителем очереди. Заявки поступают через каждые t =13 секунд. Среднее время передачи одного сообщения

t=10 секунд. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят, принимаются в очередь, не покидая ее до начала обслуживания.

Определить следующие показатели эффективности:

L оч - среднее число сообщений в очереди

L сист - среднее суммарное число сообщений в очереди и передающихся по ветви связи

Т оч - среднее время пребывания сообщения в очереди до начала передачи

Т сист - среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи

Р зан -вероятность занятости (коэффициент относительной загрузки канала с)

Q- относительную пропускную способность

А- абсолютную пропускную способность

7. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3 [(N - 1) = 3]. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность = 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.

Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме: P 0 , P 1 , P 2 , P 3 , P 4 , P отк, q,A, L оч, L сис, T оч, T сис

ЗАНЯТИЕ 4

Многоканальные СМО с ожиданием, с ожиданием и ограниченной длиной очереди

Рассмотрим многоканальную систему массового обслуживания с ожиданием. Данный тип СМО часто используется при моделировании групп абонентских терминалов ЛВС, работающих в диалоговом режиме. Процесс массового обслуживания при этом характеризуется следующим: входной и выходной потоки являются пуассоновскими с интенсивностями и соответственно; параллельно обслуживаться могут не более n клиентов. Система имеет n каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна 1/м для каждого канала. Эта система также относится к процессу гибели и размножения.

с=л/nм - отношение интенсивности входящего потока к суммарной интенсивности обслуживания, является коэффициентом загрузки системы

(с<1). Существует стационарное распределение числа запросов в рассматриваемой системе. При этом вероятности состояний Р к определяются:

где Р 0 - вероятность свободного состояния всех каналов при неограниченной очереди, k-количество заявок.

если принять с=л / м, то Р 0 можно определить для неограниченной очереди:

Для ограниченной очереди:

где m-длина очереди

При неограниченной очереди:

Относительная пропускная способность q=1,

Абсолютная пропускная способность А=л,

Среднее число занятых каналов Z=А/м

При ограниченной очереди

1 Межузловая ветвь вторичной сети связи имеет n = 4 каналов. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность = 8 сообщений в секунду. Среднее время t = 0,1 передачи одного сообщения каждым каналом связи равно t/n = 0,025 секунд. Время ожидания сообщений в очереди неограниченно. Найти характеристики СМО:

Р отк - вероятность отказа передачи сообщений;

Q - относительную пропускную способность ветви связи;

А - абсолютную пропускную способность ветви связи;

Z - среднее число занятых каналов;

L оч - среднее число сообщений в очереди;

Т ож - среднее время ожидания;

Т сист - среднее суммарное время пребывания сообщений в очереди и передачи по ветви связи.

2. Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации. Поток неисправных механизмов, прибывающих в мастерскую, - пуассоновский и имеет интенсивность = 2,5 механизма в сутки, среднее время ремонта одного механизма распределено по показательном у закону и равно = 0,5 сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно. Требуется вычислить следующие предельные значения вероятностных характеристик системы:

Вероятности состояний системы;

Среднее число заявок в очереди на обслуживание;

Среднее число находящихся в системе заявок;

Среднюю продолжительность пребывания заявки в очереди;

Среднюю продолжительность пребывания заявки в системе.

3. Межузловая ветвь вторичной сети связи имеет n=3 канала. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность л=5 сообщений в секунду. Среднее время передачи одного сообщения t=0,1 , t/n=0,033 сек.. В накопителе очереди ожидающих передачи сообщений может находиться до m= 2 сообщений. Сообщение, прибывшее в момент, когда все места в очереди заняты, получает отказ передачи по ветви связи. Найти характеристики СМО: Р отк -вероятность отказа передачи сообщений, Q-относительную пропускную способность, А- абсолютную пропускную способность, Z- среднее число занятых каналов, L оч - среднее число сообщений в очереди, Т ож - среднее время ожидания, Т сист - среднее суммарное время пребывания сообщения в очереди и его передачи по ветви связи.

ЗАНЯТИЕ 5

Замкнутая СМО

Рассмотрим модель обслуживания машинного парка, которая представляет собой модель замкнутой системы массового обслуживания. До сих пор мы рассматривали только такие системы массового обслуживания, для которых интенсивность входящего потока заявок не зависит от состояния системы. В этом случае источник заявок является внешним по отношению к СМО и генерирует неограниченный поток требований. Рассмотрим системы массового обслуживания, для которых зависит от состояния системы, при чем источник требований является внутренним и генерирует ограниченный поток заявок. Например, обслуживается машинный парк, состоящий из N машин, бригадой R механиков (N > R), причем каждая машина может обслуживаться только одним механиком. Здесь машины являются источниками требований (заявок на обслуживание), а механики - обслуживающими каналами. Неисправная машина после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание. Очевидно, что интенсивность зависит от того, сколько машин в данный момент находится в эксплуатации (N - k) и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k). В рассматриваемой модели емкость источника требований следует считать ограниченной. Входящий поток требований исходит из ограниченного числа эксплуатируемых машин (N - k), которые в случайные моменты времени выходят из строя и требуют обслуживания. При этом каждая машина из (N - k) находится в эксплуатации. Генерирует пуассоновский поток требований с интенсивностью X независимо от других объектов, общий (суммарный) входящий поток имеет интенсивность. Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным. Таким образом, в замкнутой системе массового обслуживания входящий поток требований формируется из выходящего. Состояние S k системы характеризуется общим числом требований, находящихся на обслуживании и в очереди, равным k. Для рассматриваемой замкнутой системы, очевидно, k = 0, 1, 2, ... , N. При этом если система находится в состоянии S k , то число объектов, находящихся в эксплуатации, равно (N - k). Если - интенсивность потока требований в расчете на одну машину, то:

Система алгебраических уравнений, описывающих работу замкнутой СМО в стационарном режиме, выглядит следующим образом:

Решая данную систему, находим вероятность k-гo состояния:

Величина P 0 определяется из условия нормирования полученных результатов по формулам для P k , k = 0, 1, 2, ... , N. Определим следующие вероятностные характеристики системы:

Среднее число требований в очереди на обслуживание:

Среднее число требований, находящихся в системе (на обслуживании и в очереди)

среднее число механиков (каналов), «простаивающих» из-за отсутствия работы

Коэффициент простоя обслуживаемого объекта (машины) в очереди

Коэффициент использования объектов (машин)

Коэффициент простоя обслуживающих каналов (механиков)

Среднее время ожидания обслуживания (время ожидания обслуживания в очереди)

Задача по замкнутой СМО

1. Пусть для обслуживания десяти персональных компьютеров (ПК) выделено два инженера одинаковой производительности. Поток отказов (неисправностей) одного компьютера - пуассоновский с интенсивностью = 0,2. Время обслуживания ПК подчиняется показательному закону. Среднее время обслуживания одного ПК одним инженером составляет: =1,25 час. Возможны следующие варианты организации обслуживания:

Оба инженера обслуживают все десять компьютеров, так что при отказе ПК его обслуживает один из свободных инженеров, в этом случае R = 2, N = 10;

Каждый из двух инженеров обслуживает по пять закрепленных за ним ПК. В этом случае R = 1, N = 5.

Необходимо выбрать наилучший вариант организации обслуживания ПК.

Надо опр-ть все вероятности состояний Р к: Р 1 - Р 10 , учитывая, что и используя результаты расчета Р к, вычислим Р 0

ЗАНЯТИЕ 6

Вычисление трафика.

Теория телетрафика - раздел теории массового обслуживания. Основы теории телетрафика заложил датский ученый А.К. Эрланг. Его работы были опубликованы в 1909-1928 гг. Дадим важные определения, используемые в теории телетрафика (ТТ). Термин «трафик» (англ.,traffic) соответствует термину «телефонная нагрузка». Подразумевается нагрузка, создаваемая потоком вызовов, требований, сообщений, поступающих на входы СМО. Объемом трафика называют пропущенную тем или иным ресурсом величину суммарного, интегрального интервала времени, в течение которого данный ресурс был занят за анализируемый период времени. Единицей работы можно считать секундозанятие ресурса. Иногда можно прочитать о часозанятии, а порой и просто - секундах или часах. Однако рекомендации ITU дают размерность объема трафика в эрлангочасах. Чтобы понять смысл такой единицы измерения, надо рассмотреть еще один параметр трафика - интенсивность трафика. При этом чаще говорят о средней интенсивности трафика (нагрузки) на некотором заданном пуле (наборе) ресурсов. Если в каждый момент времени t из заданного интервала (t 1 ,t 2) число занятых обслуживанием трафика ресурсов из данного набора равно А(t), то средняя интенсивность трафика будет

Величина интенсивности трафика характеризуется как среднее число ресурсов, занятых обслуживанием трафика на заданном интервале времени. Единицей измерения интенсивности нагрузки является один Эрланг (1 Эрл, 1 Е)., т.е. 1 эрланг- это такая интенсивность трафика, которая требует полной занятости одного ресурса, или, иначе говоря, при которой ресурсом выполняется работа величиной в одно секундо-занятие за время в одну секунду. В американской литературе иногда можно встретить другую единицу измерения, называемую CCS- Centrum (or hundred) Calls Second (гектосекундозанятия). Число CCS отражает время занятия серверов в 100 секундных интервалов за 1 час. Интенсивность, измеренную в CCS, можно пересчитать в Эрланги по формуле 36CCS=1 Эрл.

Трафик, создаваемый одним источником и выраженный в часо-занятиях, равен произведению числа попыток вызовов с за определенный интервал времени Т на среднюю длительность одной попытки t: у = с t (ч-з). Трафик можно вычислить тремя разными способами:

1) пусть число вызовов с в течение часа равно 1800, а средняя длительность занятия t = 3 мин, тогда Y = 1800 выз. /ч. 0,05 ч = 90 Эрл;

2) пусть в течение времени Т фиксируются длительности t i всех n занятий выходов некоторого пучка, тогда трафик определяют так:

3) пусть в течение времени Т выполняется наблюдение через равные промежутки времени за количеством одновременно занятых выходов некоторого пучка, по результатам наблюдений строят (рисунок 8) ступенчатую функцию времени x(t).

Рисунок 8. Отсчеты одновременно занятых выходов пучка

Трафик в течение времени Т может быть оценен как среднее значение х(t) за это время:

где n - число отсчетов одновременно занятых выходов. Величина Y есть среднее количество одновременно занятых выходов пучка в течение времени Т.

Колебания трафика. Трафик вторичных телефонных сетей существенно колеблется во времени. В течение рабочего дня кривая трафика имеет два или даже три пика (рисунок 9).

Рисунок 9. Колебания трафика в течение суток

Час суток, в течение которого трафик, наблюдаемый длительное время, имеет наибольшее значение, называют часом наибольшей нагрузки (ЧНН). Знание трафика в ЧНН принципиально важно, так как им определяется количество каналов (линий), объем оборудования станций и узлов. Трафик одного и того же дня недели имеет сезонные колебания. Если день недели является предпраздничным, то ЧНН этого дня выше, чем и день после праздника. Если количество служб, поддерживаемых сетью, растет, то и трафик растет. Поэтому проблематично предсказывать с достаточной уверенностью возникновение пиков трафика. Трафик внимательно отслеживается администрацией сетей и проектными организациями. Правила измерения трафика разработаны МСЭ-Т и используются администрациями национальных сетей для того, чтобы удовлетворить требованиям качества предоставляемых услуг, как для абонентов своей сети, так и для абонентов других сетей, связанных с ней. Теорию телетрафика можно использовать для практических расчетов потерь или объема оборудования станции (узла) только в том случае, если трафик стационарный (статистически установившийся). Этому условию приближенно удовлетворяет трафик в ЧНН. Величина нагрузки, поступающая за сутки на АТС, влияет на профилактику и ремонт оборудования. Неравномерность поступления нагрузки на станцию в течение суток определяется коэффициентом концентрации

Более строго определение ЧНН производится следующим образом. Рекомендация ITU Е.500 предписывает проанализировать данные об интенсивности за 12 месяцев, выбрать из них 30 наиболее загруженных дней, найти в эти дни наиболее загруженные часы и усреднить результаты измерения интенсивности на этих интервалах. Такой расчет интенсивности трафика (нагрузки) называют нормальной оценкой интенсивности трафика в ЧНН или уровнем А. более жесткой оценки можно проводить усреднение за 5 самых загруженных дней выбранного 30-дневного периода. Такая оценка носит название повышенной или оценкой по уровню В.

Процесс создания трафика. Как известно каждому пользователю телефонной сети, не все попытки установления соединения с вызываемым абонентом заканчиваются успешно. Иногда приходится делать несколько неудачных попыток, прежде чем будет установлено желаемое соединение.

Рисунок 10. Диаграмма событий при установлении соединения между абонентами

Рассмотрим возможные события при моделировании установления соединения между абонентами А и Б (рисунок 10). Статистические данные о вызовах в телефонных сетях таковы: доля состоявшихся разговоров составляет 70-50 %, доля несостоявшихся - 30-50 %. Любая попытка абонента занимает вход СМО. При удачных попытках (когда разговор состоялся) время занятия коммутационных приборов, устанавливающих соединения входов с выходами, больше, чем при неудачных попытках. Абонент может в любой момент времени прервать попытки установления соединения. Повторные попытки могут быть вызваны следующими причинами:

Номер набран неправильно;

Предположение об ошибке в работе сети;

Степень срочности разговора;

Неудачные предыдущие попытки;

Знание привычек абонента Б;

Сомнение в правильности набора номера.

Повторная попытка может быть предпринята в зависимости от следующих обстоятельств:

Степени срочности;

Оценки причины неуспеха;

Оценки целесообразности повторения попыток,

Оценки приемлемого интервала между попытками.

Отказ от повторной попытки может быть связан с низкой степенью срочности. Различают несколько видов трафика, создаваемого вызовами: поступающий (предложенный) Y п и пропущенный Y пр. Трафик Y п включает все успешные и неуспешные попытки, трафик У пр, являющийся частью Y п, включает успешные и часть неуспешных попыток:

Y пр = Y р + Y нп,

где Y р - разговорный (полезный) трафик, а Y нп - трафик, созданный неудачными попытками. Равенство Y п = Y р возможно лишь в том идеальном случае, если нет потерь, ошибок вызывающих абонентов и не ответов вызываемых абонентов.

Разность между поступающей и пропущенной нагрузками за определенный промежуток времени будет являться потерянной нагрузкой.

Прогнозирование трафика. Ограниченность ресурсов приводит к необходимости поэтапного расширения станции и сети. Администрация сети делает прогноз увеличения трафика в течение этапа развития, учитывая, что:

Доход определяется частью пропущенного трафика Y р, - затраты определяются качеством обслуживания при наибольшем трафике;

Большая доля потерь (низкое качество) бывает в редких случаях и характерна для конца периода развития;

Наибольший объем пропущенного трафика приходится на периоды, когда потери практически отсутствуют, - если потери меньше 10 %, то абоненты на них не реагируют. При планировании развития станций и сети проектировщик должен ответить на вопрос, каковы требования к качеству предоставления услуг (к потерям). Для этого нужно проводить измерения трафика потерь по принятым в стране правилам.

Пример измерения трафика.

Сначала рассмотрим, как можно отображать работу СМО, имеющую несколько ресурсов, которые одновременно обслуживают некоторый трафик. Будем далее говорить о таких ресурсах, как о серверах, которые обслуживают поток заявок или требований. Одним из наиболее наглядных и часто употребляемых способов изображения процесса обслуживания заявок пулом серверов является диаграмма Ганта (Gantt). Эта диаграмма представляет собой прямоугольную систему координат, ось абсцисс которой изображает время, а на оси ординат помечаются дискретные точки, соответствующие серверам пула. На рисунке 11 изображена диаграмма Ганта для системы с тремя серверами.

В первые три интервала времени (считаем их секундой) заняты первый и третий серверы, следующие две секунды - только третий, затем одну секунду работает второй, потом, две секунды второй и первый, и последние две секунды- только первый.

Построенная диаграмма позволяет произвести расчеты объема трафика и его интенсивности. Диаграмма отражает только обслуженный или пропущенный трафик, поскольку ничего не говорит о том, поступали ли в систему заявки, которые не смогли быть обслужены серверами.

Объем пропущенного трафика вычисляется как суммарная длина всех отрезков диаграммы Ганта. Объем за время 10 секунд:

Свяжем с каждым временным интервалом отложенным по оси абсцисс, целое число, равное количеству серверов, занятых на этом единичном интервале. Эта величина А(t) - мгновенная интенсивность. Для нашего примера

А(t)= (2, 2, 2, 1, 1, 1, 2, 2, 1, 1)

Найдем теперь среднюю за период 10 секунд интенсивность трафика

Таким образом, средняя интенсивность трафика, пропущенного рассматриваемой системой из трех серверов, равна 1,5 Эрл.

Основные параметры нагрузки

Телефонной связью пользуются различные категории абонентов, которые характеризуются:

числом источников нагрузки- N,

средним числом вызовов от одного источника за определенное время (ЧНН обычно)- c,

средней длительностью одного занятия коммутационной системы при обслуживании одного вызова- t.

Величина интенсивности нагрузки будет

Определим различные источники вызовов. Например,

Среднее число вызовов в ЧНН от одного учрежденческого аппарата;

Среднее число вызовов от одного квартирного индивидуального аппарата; случайное событие массовое обслуживание телетрафик

с кол - то же от аппарата коллективного пользования;

с ма - то же от одного монетного аппарата;

с сл - то же от одной соединительной линии.

Тогда среднее число вызовов от одного источника:

Существуют приблизительные данные для среднего числа вызовов от одного источника соответствующей категории:

3,5 - 5, =0,5 - 1, с кол = 1,5 - 2, с ма =15 - 30, с сл =10 - 30.

Различают следующие виды соединений, которые в зависимости от исхода соединения создают на станции различную по величине телефонную нагрузку:

k р - коэффициент, показывающий долю соединений, окончившихся разговором;

k з - соединения, не окончившиеся разговором из-за занятости вызываемого абонента;

k но - коэффициент, выражающий долю соединений, не окончившихся разговором по причине неответа вызываемого абонента;

k ош - соединения, не окончившиеся разговором из-за ошибок вызывающего абонента;

k тех - вызовы, не окончившиеся разговором по техническим причинам.

При нормальной работе сети значения этих коэффициентов равны:

k р =0,60-0,75; k з =0,12-0,15; k но =0,08-0,12; k ош =0,02-0,05; k тех =0,005-0,01.

Средняя длительность занятия зависит от видов соединений. Например, если соединение закончилось разговором, средняя длительность занятия приборов t сост будет равна

где - длительность установления соединения;

t сост. - состоявшийся разговор;

t в - длительность посылки вызова в телефонный аппарат вызываемого абонента;

t р - длительность разговора

где t со - сигнал ответа станции;

1,5n- время набора номера вызываемого абонента (n-количество знаков в номере);

t с - время, необходимое для установления соединения коммутационными механизмами и разъединения соединения после окончания разговора. Примерные значения рассмотренных величин:

t со =3сек., t c = 1-2,5сек., t в = 8-10сек., t р =90-130сек.

Вызовы, не окончившиеся разговором тоже создают телефонную нагрузку.

Среднее время занятия приборов при занятости вызываемого абонента равна

где t уст.соед. определяется по (4.2.3)

t зз - время слушания зуммера занятости, t зз =6сек.

Средняя длительность занятия приборов при не ответе вызываемого абонента равна

где t пв - время слушания сигнала контроля посылки вызова, t пв =20сек.

Если разговора не было из-за ошибок абонента, то в среднем t ош =30 сек.

Длительность занятий, не окончившихся разговором по техническим причинам, не определена, так как процент таких занятий мал.

Из всего выше сказанного следует, что полная нагрузка, создаваемая группой источников за ЧНН, равна сумме нагрузок отдельных видов занятий.

где - коэффициент, учитывающий слагаемые как доли

На телефонной сети с семизначной нумерацией запроектирована АТС, структурный состав абонентов которой следующий:

N учр =4000, Nинд=1000, N кол =2000, N ма =400, N сл =400.

Среднее число вызовов, поступающее от одного источника в ЧНН, равно

По формулам (4.2.3) и (4.2.6) находим нагрузку

1.10.62826767 сек.зан.=785,2чз.

Средняя длительность занятия t из формулы Y=Nct

t= Y/Nc= 2826767/7800*3.8=95.4 сек.

Задача на нагрузку

1.На телефонной сети с семизначной нумерацией запроектирована АТС, структурный состав абонентов которой следующий:

N учр =5000, Nинд=1500, N кол =3000, N ма =500, N сл =500.

Определить нагрузку, поступающую на станцию - Y, среднюю длительность занятия t, если известно, что

с учр =4, с инд =1, с кол =2, с ма =10, с сл =12, t р =120 сек., t в =10 сек., k р =0,6, t с =1 сек., =1,1.

Размещено на Allbest.ru

Подобные документы

Понятие равномерно распределенной случайной величины. Мультипликативный конгруэнтный метод. Моделирование непрерывных случайных величин и дискретных распределений. Алгоритм имитационного моделирования экономических отношений между кредитором и заемщиком.

курсовая работа , добавлен 03.01.2011


Общие понятия теории массового обслуживания. Особенности моделирования систем массового обслуживания. Графы состояний СМО, уравнения, их описывающие. Общая характеристика разновидностей моделей. Анализ системы массового обслуживания супермаркета.

курсовая работа , добавлен 17.11.2009


Элементы теории массового обслуживания. Математическое моделирование систем массового обслуживания, их классификация. Имитационное моделирование систем массового обслуживания. Практическое применение теории, решение задачи математическими методами.

курсовая работа , добавлен 04.05.2011


Понятие случайного процесса. Задачи теории массового обслуживания. Классификация систем массового обслуживания (СМО). Вероятностная математическая модель. Влияние случайных факторов на поведение объекта. Одноканальная и многоканальная СМО с ожиданием.

курсовая работа , добавлен 25.09.2014


Изучение теоретических аспектов эффективного построения и функционирования системы массового обслуживания, ее основные элементы, классификация, характеристика и эффективность функционирования. Моделирование системы массового обслуживания на языке GPSS.

курсовая работа , добавлен 24.09.2010


Разработка теории динамического программирования, сетевого планирования и управления изготовлением продукта. Составляющие части теории игр в задачах моделирования экономических процессов. Элементы практического применения теории массового обслуживания.

практическая работа , добавлен 08.01.2011


Элементарные понятия о случайных событиях, величинах и функциях. Числовые характеристики случайных величин. Виды асимметрии распределений. Статистическая оценка распределения случайных величин. Решение задач структурно-параметрической идентификации.

курсовая работа , добавлен 06.03.2012


Моделирование процесса массового обслуживания. Разнотипные каналы массового обслуживания. Решение одноканальной модели массового обслуживания с отказами. Плотность распределения длительностей обслуживания. Определение абсолютной пропускной способности.

контрольная работа , добавлен 15.03.2016


Функциональные характеристики системы массового обслуживания в сфере автомобильного транспорта, ее структура и основные элементы. Количественные показатели качества функционирования системы массового обслуживания, порядок и главные этапы их определения.

лабораторная работа , добавлен 11.03.2011


Постановка цели моделирования. Идентификация реальных объектов. Выбор вида моделей, математической схемы. Построение непрерывно-стахостической модели. Основные понятия теории массового обслуживания. Определение потока событий. Постановка алгоритмов.